为什么要有任务调度
定时任务有了依赖,就需要调度。
试想一下,如果你的定时任务并不是简单的根据时间来执行,还需要依赖某些上游任务成功后才执行,那把所有任务的执行过程画出来,大概会是这样:
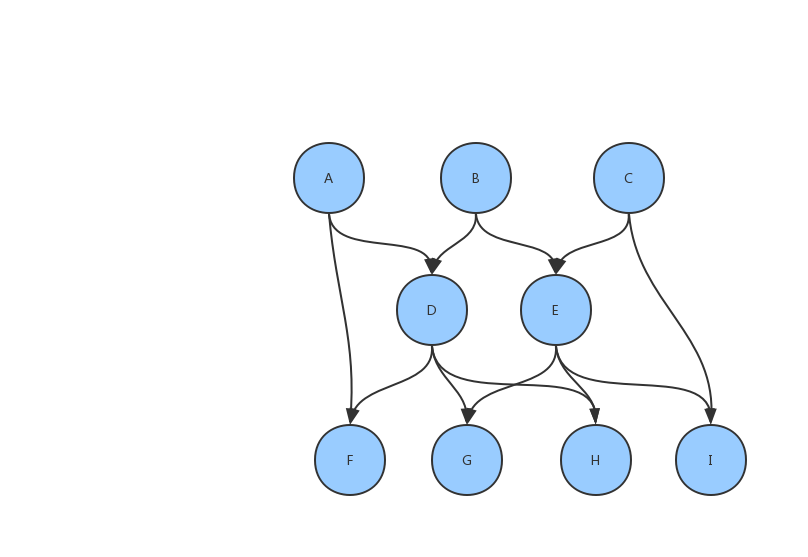
这样的图,在图论中,有一个专门的定义:
如果一个有向图从任意顶点出发无法经过若干条边回到该点,则这个图是一个有向无环图(DAG,directed acyclic graph)。
Dag 的调度可以通过使用依赖图的拓扑排序来执行,使得每个结点都仅被计算一次的情况下,所有任务都能被按正确的顺序计算。所以首先我们要将依赖图保存起来。
Mysql 中的依赖图存储
观察 Dag 图,可以简单的发现:只要我们将每一个结点的直接依赖保存,就可以将所有的偏序关系保存下来。大概是这样的:
| node | parent_node |
|---|---|
| D | A |
| D | B |
| E | B |
| E | C |
| F | A |
| F | D |
| G | D |
| G | E |
| H | D |
| H | E |
| I | C |
| I | E |
补充一下结点表:
| node |
|---|
| A |
| B |
| C |
| D |
| E |
| F |
| G |
| H |
| I |
拓扑排序
拓扑排序算法的基本步骤:
- 构造一个队列 Q(queue) 和 拓扑排序的结果队列 T(topological);
- 把所有没有依赖顶点的节点放入 Q;
- 当 Q 还有顶点的时候,执行下面步骤: 3.1 从 Q 中取出一个顶点 n(将 n 从Q中删掉),并放入 T( 将 n 加入到结果集中); 3.2 对n每一个邻接点m(n是起点,m是终点); 3.2.1 去掉边<n,m>; 3.2.2 如果m没有依赖顶点,则把m放入Q; 注:顶点A没有依赖顶点,是指不存在以A为终点的边。
这个步骤其实很好实现,根据之前 Mysql 中存储的依赖关系,可以很方便得找出没有依赖的结点,并构建一个初始队列 Q List,一个依赖关系的边 List,一个结果队列 T List,然后步骤循环执行。
并发调度
其实任务调度的时候,并不需要最后那个结果队列 T,也没有必要严格按照拓扑排序线性执行。队列 Q(执行队列)中的结点,完全可以同时并发计算。假设并发调度 Q 中的结点,有可能最后会出现 3.2.2 无法将下游的顶点 m 放入 Q 的情况。因为可能 2 个上游的 n1、n2 同时进行,判断结果对方的边还存在,所以不将 m 放入 Q。
针对上面的情况,可以考虑把判断边和放入 Q 的动作进行多次尝试。引入一个队列 R(预执行队列),将下游顶点 m 放入。不断循环 R 中的结点,并判断其是否还存在上游依赖边,没有则放入 Q。
补数据
任务调度有时候会用到对某个结点及其下游进行重跑的操作。假设我们要重跑上面的 A,那大概是这样的:
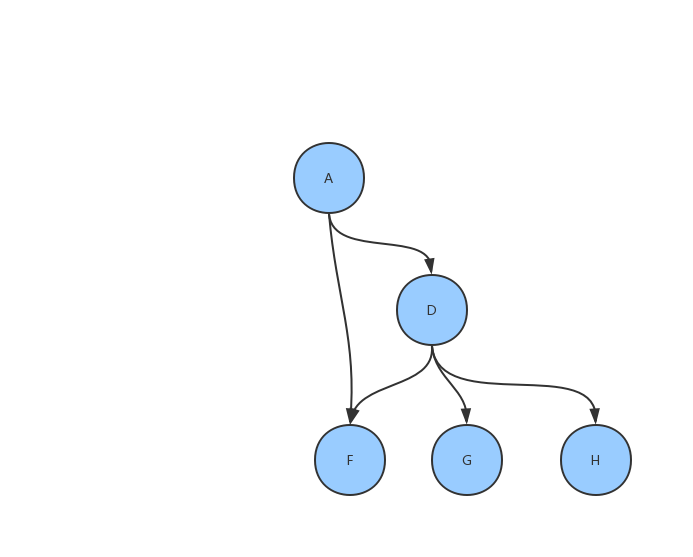
很显然,这是一个只有一个初始顶点的 DAG,完全可以用上面的方法进行调度。
这里,我主要说一下我走的弯路。
刚开始,我并没有把它当成一个 DAG,而是当成了一个不规则的树来处理(仔细看看,这其实连树都不是)。理所当然的,我定义了这样的对象:
public class Node {
private String name;
private Set<Node> childrenNodes;
private List<Set<Node>> nodesByLayer;
private Set<Node> allChildrenNodes;// 辅助用途
}
通过递归查找,可以很方便的加载到内存中,大致是这样的:
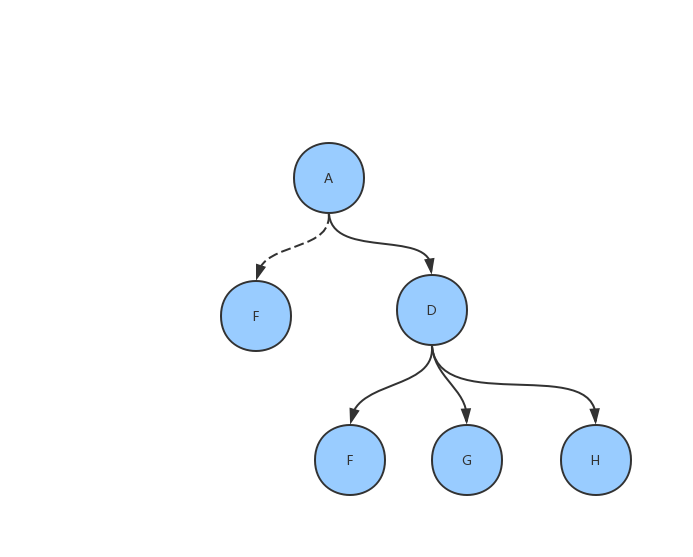
接下来就是按顺序执行,所以我定义了一个childrenNodesByLayer来保存顺序,我的想法是把这棵树转换成按层级存储,然后只要按层级执行就能保证顺序的正确性。所以我写了这样的方法:
public void generateLayers() {
this.setAllChildrenNodes(new LinkedHashSet<>());
List<Set<Node>> NodesByLayer = new LinkedList<>();
this.setNodesByLayer(NodesByLayer);
Set<Node> thisNodes = new ConcurrentHashSet<>();
thisNodes.add(this);
while (!CollectionUtils.isEmpty(thisNodes)) {
NodesByLayer.add(thisNodes);
thisNodes = this.getDirectChildren(thisNodes);
}
}
private Set<Node> getDirectChildren(Set<Node> Nodes) {
Set<Node> nextLayerNodes = new ConcurrentHashSet<>();
List<Set<Node>> NodesByLayer = this.getNodesByLayer();
Set<Node> allChildrenNodes = this.getAllChildrenNodes();
for (Node Node : Nodes) {
Set<Node> childrenNodes = Node.getChildrenNodes();
if (!CollectionUtils.isEmpty(childrenNodes)) {
for (Node childrenNode : childrenNodes) {
// 如果新的任务已经在任务Set中,将任务Set中的该任务移除
if (allChildrenNodes.contains(childrenNode)) {
for (Set<Node> confs : NodesByLayer) {
confs.removeIf(x -> x.getId().equals(childrenNode.getId()));
}
} else {
allChildrenNodes.add(childrenNode);
}
nextLayerNodes.add(childrenNode);
}
}
}
return nextLayerNodes;
}
简单来说,就是从第一层(只包含补数据开始结点)出发,不断获取该层每一个结点的下游结点,并放入下一层。
如果简单的直接放入,会出现一个结点重复出现在不同层级的情况,比如上图的 F,所以这里放入下一层前做了个简单的处理,先删除之前层里的已存在结点,然后再放入下一层。然后就遇到了ConcurrentModificationException异常,这个异常会在边遍历 Collection 边添加或删除里边的元素时发生,原因是迭代时modCount和expectedModCount不等,list.remove(o)的时候,只将modCount++,而expectedCount值未变。这里我直接使用ConcurrentHashSet了。
很显然这样的效率不高,每一次都需要判断之前层级里是否已存在,还需要进行删除操作。重新审视上面的流程,可以发现,这样的操作是事后判断,那其实也可以事前判断。可以在放入之前,先判断当前结点的邻接上游结点是否已放入,如果所有上游结点都已在allChildrenNodes中,才放入。
修改后的代码如下:
public void generateLayers() {
Set<Node> allChildrenNodes = new LinkedHashSet<>();
allChildrenNodes.add(this);
this.setAllChildrenNodes(allChildrenNodes);
List<Set<Node>> NodesByLayer = new LinkedList<>();
this.setNodesByLayer(NodesByLayer);
Set<Node> thisNodes = new LinkedHashSet<>();
thisNodes.add(this);
while (!CollectionUtils.isEmpty(thisNodes)) {
NodesByLayer.add(thisNodes);
thisNodes = this.getDirectChildren(thisNodes);
}
}
private Set<Node> getDirectChildren(Set<Node> Nodes) {
Set<Node> nextLayerNodes = new ConcurrentHashSet<>();
Set<Node> allChildrenNodes = this.getAllChildrenNodes();
for (Node Node : Nodes) {
Set<Node> childrenNodes = Node.getChildrenNodes();
if (!CollectionUtils.isEmpty(childrenNodes)) {
for (Node childrenNode : childrenNodes) {
if (CollectionUtils.isEmpty(childrenNode.getParentNodes())
|| allChildrenNodes.containsAll(childrenJobConf.getParentNodes())) {
// 如果上游所有任务都已经在已分配任务Set中,将该任务分配
nextLayerNodes.add(childrenNode);
}
}
}
}
allChildrenNodes.addAll(nextLayerNodes);
return nextLayerNodes;
}
这样以后,再重新观察流程,就会发现,这不就是上面的拓扑排序吗!嗯,真香。